金融过程中的期权定价(金融期权定价模型)

期权是一种赋予持有人在未来特定时间（到期日）以特定价格（执行价格）买入或卖出标的资产（如股票、债券、商品等）的权利，而非义务的金融衍生品。期权定价是金融工程中一个核心问题，其目标是确定一个给定期权在当前时间点的公平价格。准确的期权定价对于风险管理、投资决策和套期保值至关重要。 一个有效的期权定价模型需要考虑各种因素，包括标的资产的价格波动性、到期时间、执行价格、无风险利率以及潜在的股息收益等。 将深入探讨几种常用的金融期权定价模型。

布莱克-斯科尔斯模型 (Black-Scholes Model)

布莱克-斯科尔斯模型是期权定价领域最著名和最广泛应用的模型之一。它于1973年由费雪·布莱克和迈伦·斯科尔斯提出，并因此获得了1997年的诺贝尔经济学奖（罗伯特·默顿也因其对模型的贡献而获奖）。该模型基于一系列假设，包括：标的资产价格遵循几何布朗运动；无风险利率恒定；期权可以连续交易；没有交易成本或税收；标的资产不支付股息（虽然可以扩展到支付股息的情况）；市场是有效的。

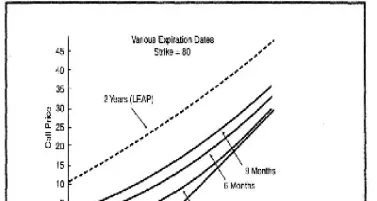
布莱克-斯科尔斯模型使用一个偏微分方程来描述期权价格随时间和标的资产价格的变化。 通过求解该方程，可以得到欧式期权（只能在到期日执行的期权）的闭式解，即一个明确的公式可以直接计算期权价格，该公式包含了所有影响期权价格的关键参数。公式如下（对于看涨期权）：

C = S N(d1) - X e^(-rT) N(d2)

其中：

• C：看涨期权价格
• S：标的资产当前价格
• X：执行价格
• r：无风险利率
• T：到期时间（以年为单位）
• N(.)：标准正态分布的累积分布函数
• d1 = [ln(S/X) + (r + σ²/2)T] / (σ√T)
• d2 = d1 - σ√T
• σ：标的资产价格的波动率

虽然布莱克-斯科尔斯模型在实际应用中非常有用，但其假设条件在现实市场中并不总是成立。例如，波动率并非恒定，市场也并非完全有效。 模型的预测结果存在误差，需要谨慎使用。

扩展的布莱克-斯科尔斯模型

为了克服布莱克-斯科尔斯模型的局限性，许多学者对其进行了扩展。这些扩展通常放松了模型的某些假设，例如：

1. 波动率微笑/倾斜： 现实市场中，波动率并非恒定，它与标的资产价格和到期时间有关。波动率微笑是指波动率与标的资产价格的关系呈现出U型曲线，而波动率倾斜是指波动率随执行价格的变化而变化。 为了解决这个问题，可以使用波动率模型来描述波动率的动态变化，例如SABR模型。

2. 股息收益： 如果标的资产支付股息，则需要在布莱克-斯科尔斯模型中考虑股息的影响。 通常通过将股息率作为参数加入模型来实现。

3. 跳跃扩散模型： 一些模型允许标的资产价格发生突然的跳跃，以更好地捕捉市场突发事件的影响。例如，梅顿跳跃扩散模型。

这些扩展模型虽然更复杂，但能够更准确地反映现实市场的情况，从而提高期权定价的精度。

二项树模型 (Binomial Tree Model)

二项树模型是一种离散时间模型，它将未来时间的期权价格分解成一系列二叉树状的步骤。在每个时间步长，标的资产的价格可以向上或向下移动到两个不同的价格水平。 通过逆向归纳法，从到期日的期权内在价值开始，逐步计算每个节点的期权价格，最终得到当前时间的期权价格。

二项树模型的优点是简单易懂，并且可以处理各种复杂的期权结构，例如美式期权（可以在到期日之前任何时间执行的期权）。 缺点是计算效率较低，尤其是在处理长到期时间或许多步长时。 通过增加时间步长数量，可以提高模型的精度，但同时也会增加计算复杂度。

蒙特卡洛模拟 (Monte Carlo Simulation)

蒙特卡洛模拟是一种基于随机抽样的数值方法，它可以用于对复杂金融衍生品的定价，包括期权。该方法通过模拟标的资产价格的随机路径来生成大量的价格路径，然后根据这些路径计算期权的最终收益，并对其进行平均，从而得到期权的期望值，即期权价格。

蒙特卡洛模拟的优点是能够处理各种复杂的模型和期权类型，包括路径依赖型期权。 缺点是计算量较大，需要较长的计算时间，而且结果的精度依赖于模拟路径的数量。

有限差分法 (Finite Difference Method)

有限差分法是一种数值方法，它将偏微分方程离散化，并通过求解差分方程来逼近期权价格。 该方法将价格空间和时间空间离散化成网格，然后使用差分方程来逼近期权价格在每个网格点的值。 通过迭代计算，最终得到当前时间的期权价格。

有限差分法的优点是精度较高，可以处理各种复杂的模型和边界条件。 缺点是计算量较大，尤其是在处理高维问题时。

总而言之，选择哪种期权定价模型取决于具体的需求和情况。 布莱克-斯科尔斯模型简单易用，但其假设条件在现实中可能不完全成立。 其他模型则通过放松某些假设或采用不同的数值方法来提高定价精度。 在实际应用中，需要根据标的资产的特性、期权的类型以及对定价精度的要求选择合适的模型。