期权定价模型发展现状(期权二叉树定价模型)

期权定价模型是金融工程领域的核心研究课题，其目的是为期权合约设定一个公平的价格。自布莱克-斯科尔斯模型(Black-Scholes model)问世以来，各种期权定价模型层出不穷，不断完善和发展。其中，二叉树定价模型作为一种相对简易且直观的模型，在教学和实际应用中都占据着重要的地位。将探讨期权定价模型的发展现状，并重点关注二叉树定价模型的原理、优势和局限性。

布莱克-斯科尔斯模型及其局限性

布莱克-斯科尔斯模型是期权定价理论的里程碑，它基于一系列假设，例如：标的资产价格服从几何布朗运动，市场无摩擦，交易连续进行，投资者可以无限制地进行借贷等等。该模型给出了欧式期权的闭式解，简洁明了，易于计算。布莱克-斯科尔斯模型的假设在现实市场中往往难以完全满足。例如，标的资产价格的波动率并非恒定不变，市场存在交易成本和税收，并且存在跳跃风险等。这些因素都会导致布莱克-斯科尔斯模型的定价结果与实际市场价格存在偏差。

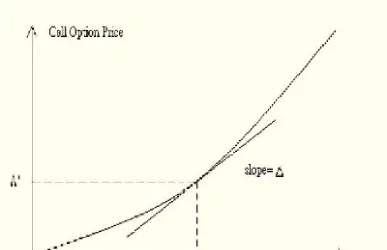
正是由于布莱克-斯科尔斯模型的局限性，促使了其他期权定价模型的出现和发展。二叉树模型就是其中一种试图克服部分布莱克-斯科尔斯模型局限性的方法。

二叉树定价模型的基本原理

二叉树模型是一种数值方法，它将期权的到期时间划分为多个小的离散时间段，并在每个时间段内假设标的资产价格只有两种可能的变化：向上或向下。通过递归地计算每个节点上的期权价值，最终得到期权在初始时间的理论价格。该模型的优点在于它能够处理一些布莱克-斯科尔斯模型无法处理的情况，例如波动率的变化和期权的早期行权。

具体而言，二叉树模型通过设定向上波动率u和向下波动率d，以及无风险利率r，来计算每个时间段内标的资产价格的向上和向下变化。利用期权的内在价值和风险中性定价原理，递归地从到期日回溯计算每个节点上的期权价值。最终，初始节点的期权价值就是模型给出的期权价格。

二叉树模型的改进与扩展

基本的二叉树模型较为简化，其精度依赖于时间段的划分数量。时间段划分越多，计算越复杂，但精度越高。为了提高精度和效率，研究者们对二叉树模型进行了改进和扩展，例如：

1. Trinomial Tree (三叉树模型): 三叉树模型允许标的资产价格在每个时间段内有三种可能的变化：向上、向下和不变。相比二叉树，三叉树能够更好地逼近标的资产价格的真实分布，提高定价精度。

2. Jump Diffusion Model (跳跃扩散模型): 将跳跃风险纳入二叉树模型，更贴近现实市场。允许标的资产价格在每个时间段内以一定的概率发生跳跃式变化。

3. Stochastic Volatility Models (随机波动率模型): 允许波动率在每个时间段内随机变化，更符合实际市场波动率的非恒定性。

二叉树模型的优势与局限性

优势：

1. 相对简单易懂，易于理解和实现。
2. 能够处理一些布莱克-斯科尔斯模型无法处理的情况，例如波动率的变化和美式期权的早期行权。
3. 可以用于定价各种类型的期权，包括欧式期权和美式期权。
4. 可以相对容易地扩展到更复杂的模型，例如考虑随机波动率或跳跃风险。

局限性：

1. 精度依赖于时间段的划分数量，计算量较大，尤其在处理长期间期权时。
2. 对参数的敏感性较高，参数估计的误差会影响定价结果。
3. 在处理高维问题时，计算复杂度会急剧增加，例如多资产期权的定价。

二叉树模型的应用

二叉树模型在实际应用中具有广泛的用途，例如：

1. 教学：作为一种直观的期权定价方法，二叉树模型常用于教学，帮助学生理解期权定价的基本原理。
2. 风险管理：可以用于估算期权的风险敞口，帮助投资者进行风险管理。
3. 套期保值：可以用于设计套期保值策略，降低投资风险。
4. 期权定价：虽然精度不如蒙特卡洛模拟等方法高，但在一些情况下，二叉树模型的计算速度和简便性使其成为一种可行的期权定价方法。

未来发展方向

尽管二叉树模型已经取得了显著的进展，但其仍存在一些局限性。未来的研究方向可能包括：

1. 开发更高效的算法，提高计算速度和精度。
2. 将二叉树模型与其他先进的模型相结合，例如神经网络模型，以提高模型的预测能力。
3. 研究更复杂的市场环境下的二叉树模型，例如考虑交易成本、税收和市场冲击等因素。

总而言之，二叉树定价模型作为一种经典的数值方法，在期权定价领域发挥着重要作用。虽然它并非完美的模型，但其简洁性、直观性和可扩展性使其在教学、研究和实际应用中都具有重要的价值。未来的研究将继续致力于改进和完善二叉树模型，使其更好地适应日益复杂和动态的金融市场。